Instabilités, Ondes et Turbulence
Les écoulements naturels et industriels, en géophysique, en aéronautique ou en génie des procédés, sont complexes, instationnaires, parfois multiphasiques, et le plus souvent turbulents. Comprendre et modéliser ces écoulements constituent un véritable défi, aux enjeux à la fois fondamentaux et pratiques.
À l'échelle de la planète, les écoulements atmosphériques et océaniques sont soumis à des effets de stratification et de rotation d'ensemble. Ces effets conduisent notamment à l'existence d'ondes internes, ainsi qu'à l'émergence de tourbillons ou de jets cohérents pouvant influencer profondément les propriétés de mélange (chaleur, polluants...)
À échelle plus petite, les écoulements avec interfaces (soit entre deux liquides, soit entre un liquide et un gaz) constituent un autre exemple de tels écoulements complexes. La formation de la houle en mer illustre bien l'étendue des questions ouvertes, qu'il s'agisse de l'origine des premières rides sous l'effet du vent, de leur amplification, ou encore des mécanisme de saturation et de dissipation par déferlement. D'autres exemples sont l'instabilité d'enroulement des "cordes liquides" qui tombent sur une surface, ou encore la morphologie surprenante des "membranes liquides" qui se forment à l'embouchure d'un tuyau horizontal.
Dans cet axe de recherche, nous développons des expériences modèles, visant à reproduire ces écoulements complexes depuis les premiers stades d'instabilités jusqu'aux situations pleinement turbulentes, dans des configurations simples et contrôlées.
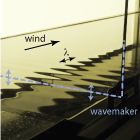
Des vagues sur une mer d'huile
Pourquoi le vent lève-t-il des vagues sur la mer ? Cette question, centrale en mécanique des fluides, a fait l'objet de décennies d'expériences et de théories. Nous abordons cette question sous un angle original : le vent ici souffle sur une mer d'huile, au sens propre ! Le fait d'utiliser un liquide plus visqueux que l'eau, en modifiant les propriétés des toutes premières ondes, nous renseigne sur les mécanismes physiques à l'origine de ce phénomène.
En savoir plus 

Des flotteurs dans la vague
Comment s'oriente un bateau balloté dans une vague ? En plus de dériver, un flotteur a tendance à s'orienter soit parallèlement, soit perpendiculairement à la crête des vagues. Pourquoi ? Il s'agit d'un subtile effet non-linéaire, que nous tentons d'éclaircir par une combinaison d'expériences, de simulations numériques et de théorie asymptotique.

Faire des plis en soufflant sur un liquide
Lorsque le vent souffle à la surface d'un liquide, il est bien connu qu'il se forme, au-delà d'une vitesse seuil, des ondes propagatives. Mais qu'advient-il lorsque le fluide est très visqueux (100 à 1000 fois plus visqueux que l'eau), au point que ces ondes propagatives deviennent amorties de manière critique ? On constate expérimentalement que les ondes se déstabilisent violemment sous forme de "plis liquides" très localisés, à la manière d'un tissu formant des plis devant un fer à repasser. Une fois formés, ces plis liquides avancent à grande vitesse, poussés par le vent.

Des spirales de Fermat dans un système diphasique aqueux
L'interaction entre un sel
et un tensioactif anionique génère des gradients de tension superficielle, qui entraînent un processus de transport
en surface (effet Marangoni). Ce transport provoque l'ascension et l'enroulement d'un filament issu d'une
gouttelette d'eau salée et la formation d'un intriguant motif en spirale de Fermat à la surface. Cet enroulement ascendant du filament induit par la convection de Marangoni pourrait
inspirer la fabrication de fibres.

Le rideau de Torricelli : Morphologie des jets laminaires sous gravité
Bien que la forme d'un jet qui jaillit horizontalement d'un orifice
ait été etudiée par Toricelli (1643), ce problème classique de la mécanique
des fluides peut encore nous surprendre. Lorsqu'un jet laminaire jaillit de l'embouchure d'un tuyau, il se divise en deux jets, l'un primaire et l'autre secondaire,
reliés par un mince rideau vertical de fluide.
Nous étudions ce comportement inattendu en utilisant des expériences de
laboratoire couplées à des simulations numériques.
En savoir plus 
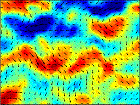
Turbulence d'ondes internes dans les fluides stratifiés et en rotation
La stratification en densité des fluides et la rotation de la Terre sont deux ingrédients clés de la dynamique des océans et de l'atmosphère. Ceux-ci modifient profondément la turbulence en permettant la propagation d'ondes internes dans le volume du fluide.
Au FAST, nous cherchons à décrire les régimes turbulents où ces ondes internes dominent l'écoulement. Dans le cadre de la "Simons Collaboration on Wave Turbulence" (2019-2026),
nous avons ainsi réalisé en 2020 la première observation expérimentale de la turbulence d'ondes dans un fluide en rotation.
Nous venons plus récemment de publier un travail théorique sur la turbulence d'ondes internes de gravité conduisant à des solutions en accord avec les observations océaniques. Ce type de modèle pourrait permettre de rendre compte de la dynamique des petites échelles océaniques dans les modèles climatiques. Nous travaillons actuellement à atteindre en laboratoire ce régime pour tester la validité des prédictions théoriques.

Sprays chargés électriquement
Les liquides peu conducteurs peuvent se charger électriquement lorsqu'ils sont pulvérisés, ce qui entraîne
une répulsion inter-gouttelettes qui limite leur coalescence et influence la
forme du panache de pulvérisation. Avec une combinaison d'expériences de laboratoire
et une théorie de couche limite, nous montrons que le courant mesuré est parfaitement décrit
par une courbe universelle en fonction de la
vitesse du liquide sur quatre ordres de grandeur. Des simulations numériques avec un simple
modèle de répulsion intergouttelettes donne des prédictions précises de la divergence
du panache de pulvérisation.

Oscillations en chaîne
Lorsqu'un jet d'eau sort d'un orifice elliptique, il se forme une structure
en forme de chaîne causée par des oscillations capillaires et inertielles.
Nous avons étudié ce phénomène à l'aide d'
une combinaison d'expériences de laboratoire, de théorie
et de simulation numérique directe. Nous constatons que
la fréquence d'oscillation n'est pas en accord avec une théorie linéaire due à Rayleigh (1879),
mais s'accorde en revanche avec une théorie non linéaire étendue due à Bohr (1909).
| 





