Instabilities, Waves and Turbulence
Natural and industrial flows, in geophysics, aeronautics or process engineering, are complex, unsteady, sometimes multiphase, and most often turbulent. Understanding and modeling these flows is a real challenge for both fundamental and practical reasons.
On a global scale, atmospheric and oceanic flows are subject to stratification and background rotation effects. These lead to the generation of internal waves, which have a profound influence on the flow dynamics, such as the emergence of eddies or coherent jets that can influence the mixing properties (heat, pollutants ...)
On a smaller scale, flows with interfaces (either between two liquids or between a liquid and a gas) provide other examples of such complex flows. The formation of ocean waves illustrates the wide range of open issues, from the origin of the first ripples generated by wind to their amplification to the mechanism of saturation and dissipation by wave breaking. Other examples are the coiling instability of "liquid ropes" that fall on a surface and the surprising morphology of the "liquid curtains" that form at the exit of a horizontal pipe.
In this research group, we develop model experiments in simple and controlled configurations that aim to reproduce these complex flows from the first stages of instability to fully turbulent situations.

Making folds by blowing on a liquid
When the wind blows on the surface of a liquid, it is well known that, above a critical wind velocity, a propagative wave is formed. But what happens when the fluid is very viscous (100 to 1000 times more viscous than water), to the point that these propagative waves become critically damped? Experimentally, we observe that the waves are violently destabilized in the form of sharp "liquid folds", like a fabric forming folds in front of an iron. These liquid folds then advance at high speed, pushed by the wind, and can interact with each other.

Chain oscillations in liquid jets
A jet of water issuing vertically from an elliptical nozzle forms a
chainlike structure caused by inertial-capillary oscillations of material
cross-sections of the jet. We have studied this phenomenon using
a combination of laboratory experiments, nonlinear theory,
and direct numerical simulation. We find that the oscillation
frequency does not agree with a linear theory due to Rayleigh (1879),
but does agree with an extended nonlinear theory due to Bohr (1909).
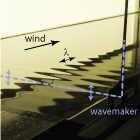
Oil waves
Why does the wind create waves on the sea? This question, central to fluid mechanics, has been the subject of decades of experiments and theories. We approach this question from a unique perspective: the wind, in this case, blows over a layer of oil. By using a liquid more viscous than water and modifying the properties of the very first waves, we shed new light on the physical mechanisms behind this phenomenon.
Read more 

Self-charging of sprays
Poorly conducting liquids can undergo self-charging during spraying, leading
to inter-droplet repulsion that prevents coalescence and influences the
shape of the spray plume. Using a combination of laboratory experiments
and boundary-layer theory, we show that measurements of the streaming
current collapse onto a universal curve as a function of the dimensionless
liquid velocity over four decades. Numerical simulations with a simple
model for interdroplet repulsion yield accurate predictions of the divergence
of the spray plume.

Fermat's spiral patterns in an aqueous two-phase system
The interaction between a salt
and an anionic surfactant generates surface tension gradients, which drive a transport process
at the surface (Marangoni effect). This transport consists of the rising and coiling of a filament from a droplet located at the bottom of a bulk solution, resulting in an intriguing Fermat's spiral pattern on the surface. The
bottom-up coiling of the filament, driven by Marangoni convection, may
inspire automatic fiber fabrication.

Torricelli's curtain: Morphology of laminar jets under gravity
While the form of a fluid jet issuing horizontally from an orifice
was first studied by Torricelli (1643), this classic problem in fluid
mechanics still holds surprises. When a laminar jet issues from the
end of a pipe, it divides into primary and secondary
jets with a thin vertical curtain of fluid connecting them.
We are currently using laboratory experiments and numerical
simulations to study this unexpected behavior.
Read more 
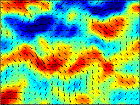
Internal wave turbulence in stratified and rotating fluids
The stratification in density of the fluid and the Earth rotation are two key ingredients in the dynamics of the oceans and atmosphere. They profoundly modify the turbulence by allowing the propagation of internal waves in the volume of the fluid. At FAST lab, we seek to describe the turbulent regimes where these internal waves dominate the flow. As part of the "Simons Collaboration on Wave Turbulence" (2019-2026), we achieved in 2020 the first experimental observation of a wave turbulence regime in a rotating fluid. We more recently published a theoretical work on the turbulence of internal gravity waves leading to solutions in line with oceanic observations. This type of model could make it possible to account on a physical basis for the dynamics of the small oceanic scales in climate models. We are currently working on achieving this regime in the laboratory to test the validity of the theoretical predictions.

Floaters drifting in waves
How does a boat drifting in a wave orient itself? Experiments show that it tends to orient itself either parallel or perpendicular to the wave crest. Why? This is a subtle non-linear effect, which we attempt to elucidate through a combination of experiments, numerical simulations and asymptotic theory.
| 





