Laboratoire FAST, Orsay
Version PDF (300 Ko)
Depuis les galaxies spirales jusqu'à votre tasse de thé du matin, en passant par la circulation atmosphérique ou océanique, les écoulements en rotation sont très fréquents dans la nature. Outre l'intérêt que les astrophysiciens ou les météorologues - ou tout simplement ceux qui aiment à contempler les phénomènes naturels - peuvent y porter, ces écoulements jouent également un rôle majeur dans nombre d'applications industrielles ou pratiques.
La rotation de la Terre fournit sans doute les observations les plus surprenantes des écoulements en rotation. À la fin du XIXème siècle, à l'heure des premières expéditions polaires, l'océanographe norvégien Nansen observa que la dérive des icebergs ne suivait pas, comme on aurait pu s'y attendre, la direction du vent, mais était systématiquement déviée vers la droite. L'explication de ce phénomène fut apportée dans les années 1905 par le physicien suédois Walfrid Ekman, qui y vit l'influence de la force de Coriolis. En effet, pour un observateur lié à la Terre en rotation, un mouvement rectiligne apparaîtra comme une trajectoire courbe, déviée vers la droite dans l'hémisphère Nord (Figure 1). Ainsi le vent, en entraînant les masses d'eau sur une certaine profondeur, d'une centaine de mètres environ, leur imprime une déviation vers la droite : c'est là l'origine des grandes circulations océaniques, expliquant du même coup l'étrange trajectoire des icebergs !
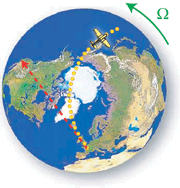
Figure 1 : Pas trop loin du pôle, la Terre peut
être assimilée à un manège tournant à
vitesse angulaire W = 2p
/ T = 7.10-5 s-1 (où T=24 h).
Un avion sans pilote joignant Paris à Los Angeles selon une trajectoire
rectiligne (flèche rouge) par rapport à un référentiel
extérieur verra sa trajectoire déviée vers la droite
pour un observateur lié à la Terre (faites pivoter votre
Bulletin !). Le pilote impuissant, resté au sol, imputera à
la "force de Coriolis" cette déviation de la trajectoire...
Tournons-nous vers une expérience sans doute plus proche de notre quotidien. Peut-être avez-vous été étonnés en constatant, après avoir remué votre thé ou votre tisane, que les débris de feuilles ou autres petits résidus solides plus denses que l'eau étaient ramenés vers le centre de la tasse. Vous vous seriez probablement attendus à les voir au contraire repoussés vers l'extérieur sous l'effet de la force centrifuge ! Ce "paradoxe" s'explique par le frottement du fluide sur le fond de la tasse, qui diminue la vitesse de rotation du fluide. La force centrifuge, variant comme le carré de la vitesse de rotation, est donc plus faible au fond de la tasse que sur le reste de la hauteur. Ce déséquilibre induit un écoulement de recirculation vers le centre au fond de la tasse et, par conservation de la masse, vers l'extérieur dans le reste de la hauteur (voir la Figure 2). Cette circulation centripète du fluide porte le nom de couche de Bödewadt (1940), du nom du mécanicien des fluides allemand qui a décrit la situation idéalisée d'un fluide en rotation uniforme au-dessus d'une paroi immobile infinie. Mais c'est Albert Einstein le premier qui, en 1926, propose une explication qualitative de ce phénomène dans le cas de la tasse de thé1 !
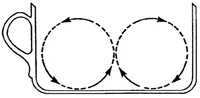
Figure 2 : Figure originale d'Einstein en introduction
de son article de 1926 portant sur la formation des méandres dans
les fleuves. Les flèches en pointillé représentent
l'écoulement de recirculation qui accompagne la rotation d'un fluide,
responsable du rassemblement des feuilles de thé au centre de la
tasse.
La zone de fluide ralentie par le frottement sur la paroi porte le nom de couche limite, et joue un rôle clé en mécanique des fluides (Figure 3). Son épaisseur, notée d, est la distance sur laquelle la rotation imposée W est diffusée sous l'effet de la viscosité dans les couches intermédiaires du fluide. Dans le cas idéalisé d'un fluide en rotation au-dessus d'une paroi infinie, on peut montrer que d ~ (n/W)1/2 (où n est la viscosité cinématique du fluide)2, qui est une constante sur toute la surface du disque, et dans laquelle n'intervient pas en particulier la distance r à l'axe de rotation. On parle alors de solution auto-similaire, c'est-à-dire que le profil de vitesse reste identique à lui-même par changement d'échelle de notre problème. Notons ici que, selon la situation que l'on cherche à décrire, W pourra désigner soit la vitesse angulaire du fluide, de la paroi, ou plus généralement la vitesse relative de l'un par rapport à l'autre. Dans le cadre de cette description autosimilaire, puisque l'épaisseur de la couche limite est la seule échelle de longueur du problème, on doit s'attendre à ce que tous les phénomènes physiques interviennent sur des distances caractéristiques de l'ordre de d.
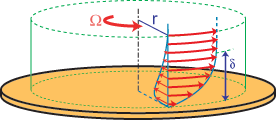
Figure 3 : Le mouvement d'un fluide se trouve freiné
au voisinage d'une paroi immobile, sur une épaisseur de l'ordre
de d (épaisseur de couche limite). C'est
sur cette même épaisseur d que
prend place l'écoulement de recirculation centripète représenté
en Figure 2.
En revanche, lorsque le disque et/ou le fluide ne s'étendent pas à l'infini, d'autres échelles de longueur peuvent intervenir, comme le rayon de la tasse par exemple, ou encore la hauteur de fluide. Dans ce cas, qu'advient-il des solutions autosimilaires ? Si l'on suppose la situation la plus simple où le volume fini du fluide est confiné entre deux disques tournants (le disque supérieur pouvant jouer le rôle de la surface libre du fluide), on peut supposer en toute généralité l'existence de deux couches limites, centrifuge au voisinage du disque le plus rapide et centripète près du plus lent ! De ce problème apparemment simple, aucune solution analytique n'est pourtant connue, tant les équations du mouvement sans hypothèse de similitude, même en régime stationnaire, s'avèrent compliquées. Ce problème a d'ailleurs donné lieu à une célèbre controverse de l'histoire de la mécanique des fluides : George Batchelor (1951) était partisan d'une solution à deux couches limites séparant une zone centrale en rotation solide, tandis que Keith Stewartson (1953) défendait une solution à couche limite unique. Ce n'est que plus tard que fut montré que toute une classe de solutions, incluant celles de Batchelor et Stewartson, pouvait coexister dans cet écoulement.
La stabilité des écoulements
en rotation est un sujet très vaste, lié à un grand
nombre d'applications. Citons par exemple le cas des disques durs d'ordinateurs
: cet empilement de disques en rotation rapide entraîne une mince
couche d'air interstitielle, dont les instabilités peuvent induire
des vibrations, et donc un risque d'endommagement par contact avec la tête
de lecture. Ce problème de stabilité des écoulements
tournants est très délicat, du fait de deux effets antagonistes
:
- Un effet stabilisant,
lié à une décroissance des perturbations selon la
direction de l'axe de rotation ; ainsi la rotation tend à bidimensionnaliser
l'écoulement.
- Des effets déstabilisants,
liés à un déséquilibre des forces centrifuges,
à cause par exemple du frottement aux parois (comme dans le cas
de la tasse de thé) ; on parle alors d'instabilités centrifuges.
Ces difficultés rendent quasiment impossible une recherche de solutions exactes. Dans ce contexte, les expériences ou les simulations numériques s'avèrent indispensables pour étudier la stabilité des écoulements tournants, en s'appuyant sur une analyse en termes de mécanismes physiques élémentaires. Ce domaine de recherche est particulièrement actif en France, tant du point de vue numérique qu'expérimental, à Marseille (groupes de P. Le Gal à l'IRPHE et de P. Bontoux au LMSNM), à Lille (groupe de D. Buisine au LML) et en région parisienne (groupe de P. Le Queré au LIMSI, et d'O. Daube à l'Université d'Evry).
Une expérience de disques en rotation
Afin d'étudier les instabilités de l'écoulement entre deux disques tournants, nous avons mis au point au laboratoire FAST à Orsay le dispositif expérimental représenté en Figure 4. Il est constitué de deux disques en vis-à-vis, chacun de rayon R=14 cm et distants d'une épaisseur h pouvant varier entre quelques mm et 3 cm environ. Le disque supérieur constitue le couvercle d'un récipient cylindrique en rotation, dans lequel peut tourner indépendamment le disque inférieur. Ce disque supérieur est en verre, ce qui nous permet de visualiser l'écoulement par le dessus. La visualisation est rendue possible en ensemençant l'eau de petites paillettes microscopiques. En suivant l'écoulement, les paillettes s'orientent selon la structure du champ de vitesse, et donnent lieu à des variations de l'intensité de la lumière réfléchie. Ainsi, sur les visualisations présentées dans les figures qui suivent, les zones claires correspondent à des paillettes majoritairement horizontales, tandis que les zones sombres à des paillettes plutôt verticales.
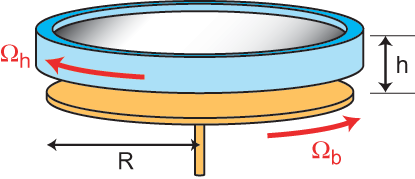
Figure 4 : Dispositif expérimental. Le disque
supérieur est transparent, afin de permettre la visualisation de
l'écoulement. Il est solidaire du cylindre extérieur (en
bleu). Le disque inférieur, en orange, est distant du disque supérieur
d'une hauteur h, entre quelques mm et 3 cm environ. Sur ce shéma
le disque inférieur a été décalé vers
le bas pour des raisons de lisibilité.
Chaque disque tourne avec sa propre vitesse angulaire, Wh et Wb. On appelle corotation l'écoulement obtenu lorsque les deux disques tournent dans le même sens (Wh et Wb de même signe) ; les instabilités de cet écoulement corotatif sont présentées dans un premier temps. L'écoulement contra-rotatif, lorsque les deux disques tournent en sens opposé, donne lieu à des phénomènes bien plus compliqués, que nous décrirons dans une seconde partie.
Instabilités de couche limite
Commençons par observer l'écoulement lorsqu'un seul des deux disques, le disque supérieur, est en rotation (Wh non nul et Wb = 0). Nous nous limitons ici à un espace interdisque faible, de h=7 mm. En augmentant progressivement la vitesse du disque supérieur depuis 0, rien n'apparaît au début : les paillettes réfléchissent la lumière uniformément. L'écoulement est dans ce cas doublement symétrique : il est invariant par rapport à toute rotation (axisymétrie) mais aussi par rapport à toute "translation" dans le temps (stationnarité). Puis, au-delà d'une certaine vitesse, une première instabilité apparaît, sous forme de cercles se propageant de l'extérieur vers l'intérieur. Ces cercles correspondent à des tourbillons annulaires. Dans ce cas, l'écoulement a perdu sa symétrie temporelle (il est instationnaire), mais a conservé sa symétrie circulaire. Si l'on augmente encore la vitesse de rotation, une seconde instabilité apparaît sous la forme d'un motif spiralé, comme le montre la Figure 5. Ce réseau de spirales tourne lui aussi, dans le même sens de rotation que le disque mais à vitesse inférieure. Cette fois-ci, l'axisymétrie est elle aussi brisée. Nous appelons par convention ce motif spirales positives, car elles s'enroulent de l'extérieur vers le centre selon la direction du disque en rotation.

Figure 5 : Spirales positives (à l'extérieur)
et cercles (à l'intérieur). On compte ici 37 bras spiraux.
Une observation précise de la Figure 5 permet d'en déduire des informations sur la nature des instabilités responsables de l'apparition de ces structures. On constate que les bras spiralés n'occupent pas toute l'extension de l'écoulement, mais ne sont présents qu'au-delà d'un certain rayon r0. Nous avons montré que ce rayon correspond à l'endroit où les couches limites associées à chacun des disques se rejoignent. En d'autres termes, pour r > r0, là où apparaissent les spirales positives, les couches limites sont séparées, alors que pour r < r0 l'écoulement est dominé par les effets de viscosité sur toute l'épaisseur, et il n'existe plus de couche limite à proprement parler. Cette observation montre que les spirales positives ne peuvent exister que dans les couches limites de l'écoulement, suggérant qu'elles naissent d'une instabilité de couche limite. Des observations complémentaires, au moyen de visualisations dans un plan perpendiculaire aux disques, nous ont permis de confirmer cette hypothèse, permettant de conclure que les spirales positives (ainsi que les cercles) naissaient d'une instabilité de la couche limite centripète près du disque inférieur.
Que se passe-t-il maintenant si le second disque, le disque inférieur, est lui aussi mis en rotation ? Vu du référentiel lié à ce disque inférieur, on peut se ramener à la situation où seul tournerait le disque supérieur à la vitesse relative DW = Wh - Wb. Ainsi, les seuils d'apparition des cercles et spirales positives précédemment décrits se trouveraient simplement décalés d'une quantité Wb. Malheureusement, cette description est quelque peu naïve, la dynamique dans un référentiel tournant ne se ramenant pas si simplement à celle dans un référentiel fixe ! Afin de rendre compte de la nature non Galiléenne du référentiel lié au disque tournant, il faut inclure la force de Coriolis. Comment nos seuils d'instabilité se trouvent-ils affectés par cette force d'inertie ?
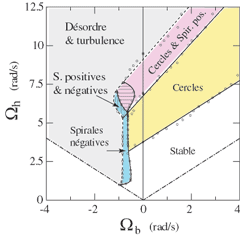
Figure 6 : Cartographie des différents motifs d'instabilité de l'écoulement dans le cas h=7 mm. La moitié droite (Wb>0) correspond à la configuration co-rotative, et la moitié gauche (Wb<0) contra-rotative.
Nous avons représenté, en Figure 6, un diagramme résumant nos observations lorsque les deux disques sont en rotation. Les axes horizontaux et verticaux représentent respectivement les vitesses angulaires de rotation des disques inférieur et supérieur. Wh est choisi toujours positif, tandis que Wb peut être positif dans le cas co-rotatif (moitié droite du diagramme) ou négatif dans le cas contra-rotatif (moitié gauche). Les deux lignes pointillées obliques représentent les vitesses égales : Wh = Wb à droite (rotation solide) et Wh = - Wb à gauche (exacte contra-rotation). La ligne verticale, à Wb = 0, correspond à l'écoulement décrit précédemment pour lequel seul tournait le disque supérieur.
Sur ce diagramme, nous constatons comme attendu que la mise en rotation du disque inférieur décale les seuils des instabilités : les frontières délimitant la région d'existence des cercles (région jaune) et des spirales positives (région rose) présentent une pente positive à Wb croissant. Ces pentes sont toutefois différentes pour ces deux structures, ce que l'on peut interpréter en termes de symétries. Les seuils d'apparition des cercles se déduisent de la ligne de rotation solide Wh = Wb par un simple décalage vertical, signifiant que le paramètre contrôlant cette instabilité est tout simplement la vitesse relative DW = Wh - Wb, sans aucune influence de la rotation globale. En d'autres termes, l'instabilité responsable de l'apparition des cercles n'est pas influencée par la nature non Galiléenne du référentiel tournant, c'est-à-dire par la force de Coriolis. En revanche, les seuils d'apparition des spirales positives, qui elles brisent l'axisymétrie de l'écoulement de base, présentent une pente supérieure à celle de la ligne de rotation solide : cette fois-ci, la vitesse relative DW = Wh - Wb n'est pas suffisante pour décrire l'apparition de ces structures, une "sur-vitesse" du disque supérieur étant nécessaire à l'apparition des spirales positives. Cette fois-ci, la rotation d'ensemble semble bien jouer son rôle de stabilisation évoqué en introduction, en retardant l'apparition de ces structures.
Instabilités de cisaillement
Nous avons jusqu'à présent restreint notre description à la partie droite du diagramme de la Figure 6, c'est-à-dire à la partie corotative (Wb > 0) et faiblement contrarotative (environ Wb > - 0,5 rad/s pour cette épaisseur interdisque). Le scénario précédent se trouve quelque peu modifié dès lors que l'on s'intéresse à un régime contra-rotatif plus prononcé, pour lequel un nouveau type de structure fait son apparition, comme le montre la Figure 7. Il s'agit là encore d'un réseau de spirales, mais elles sont à bien des égards différentes des précédentes, comme nous allons le voir. Tout d'abord, elles s'enroulent vers le centre dans le sens opposé à celui du disque tournant le plus rapidement ; pour cette raison nous les avons appelées spirales négatives. Elles correspondent aux régions bleues du diagramme de la Figure 6.

Figure 7 : Spirales négatives, pour h=7
mm. Leur sens d'enroulement vers le centre est opposé à la
rotation Wh
du disque supérieur (disque le plus rapide).
Une première observation remarquable concernant les spirales négatives est l'extrême lenteur avec laquelle elles apparaissent : une fois atteinte la valeur seuil de l'instabilité, il faut attendre parfois jusqu'à une dizaine de minutes avant de voir le motif se former. Pour cette raison, la détermination précise du seuil d'apparition est une tâche très délicate, qui nécessite un dispositif d'une grande stabilité ainsi que... beaucoup de patience ! Si l'on se place légèrement au-delà de cette valeur seuil, on constate que ce temps d'apparition devient plus raisonnable, de l'ordre de la minute voire de la dizaine de seconde ; on peut montrer en fait que ce temps d'apparition diverge à la valeur seuil3. Il est d'ailleurs possible de tirer profit de cette divergence pour déterminer avec précision la valeur du seuil, en extrapolant la tendance des temps d'apparition au-delà du seuil.
Que se passe-t-il maintenant si nous faisons varier la distance entre les deux disques ? Sur la Figure 8 on voit ce que deviennent les spirales négatives lorsqu' est augmenté l'espace interdisque à une épaisseur h = 2 cm : elles sont clairement très différentes de celles présentées en Figure 7 à faible espace (h=7 mm). L'instabilité donne maintenant lieu à une structure plus complexe au centre, ainsi qu'à un plus petit nombre de bras spiraux : alors qu'on observait 9 à 11 bras dans le cas d'un faible espace, seuls 5 bras sont visibles ici (pouvant diminuer jusqu'à deux bras seulement en augmentant encore h). Cette variation se comprend bien, si l'on se représente ces bras comme des tourbillons organisés radialement, et si l'on suppose que leur diamètre correspond approximativement à l'épaisseur interdisque.
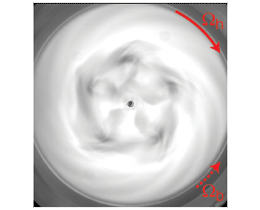

Figure 8 : Exemple de spirales négatives à 5 bras observées à grand espace interdisque (h=20 mm), et champs de vitesse correspondant, obtenu par Vélocimétrie par Images de Particules.
Dans le cas d'un espace interdisque important, il nous a été possible de réaliser des mesures de vitesse grâce à un dispositif de Vélocimétrie par Images de Particules (PIV). Cette méthode consiste à mesurer localement la distance parcourue par de petites particules entre deux images successives, permettant de reconstruire le champ de vitesse instantané dans le plan de l'image. Les particules sont éclairées au moyen d'une tranche de lumière Laser pulsée, synchronisée avec une caméra vidéo de haute sensibilité. Dans la Figure 8 est représenté le champ de vitesse obtenu par cette technique dans le cas du motif à 5 bras spiraux. Les couleurs représentent le taux de rotation local des petits éléments de fluide (vorticité), et permettent de distinguer clairement 5 tourbillons (en bleu) tournant en sens opposé à la rotation globale du disque supérieur (en rouge). Cette technique de mesure nous permet d'accéder à des informations précieuses pour la compréhension des instabilités en écoulements tournants.
On peut se demander pour finir quel est le mécanisme d'instabilité responsable de l'apparition des spirales négatives : s'agit-il d'une instabilité de couche limite, comme pour les spirales positives ou les cercles ? ou plutôt d'un nouveau mécanisme, comme une instabilité de la couche de cisaillement interdisque ? En fait, nos expériences à différents espaces interdisques nous permettent de répondre à cette question. En effet, à vitesses de disques égales, les épaisseurs des couches limites restent inchangées (d ~ (n/W)1/2 est indépendant de h), tandis que l'intensité du cisaillement (variation verticale de vitesse horizontale, de l'ordre de R DW / h), elle, diminue à mesure qu'augmente l'épaisseur h. Plaçons-nous dans le référentiel tournant à la vitesse moyenne (Wh + Wb)/2 : on obtient là une situation symétrique dans laquelle chaque disque tend à entraîner une demi-épaisseur de fluide à vitesse angulaire relative +DW/2 et -DW/2 (voir le schéma en Figure 9). À vitesse suffisamment élevée, la couche de cisaillement entre les deux disques peut devenir instable, et s'enrouler selon des lignes de tourbillon orientées radialement. Pour qu'une telle instabilité ait le temps de se développer, son temps caractéristique d'advection (de l'ordre de h / RW), doit être inférieur au temps sur lequel la viscosité va pouvoir amortir la perturbation (temps de diffusion visqueuse sur l'épaisseur, soit h2/n). Dans cette hypothèse, le rapport de ces deux temps caractéristiques (W R h /n), qui mesure l'importance de l'effet déstabilisant comparé à l'amortissement, doit donc être le paramètre contrôlant l'apparition des spirales négatives. Or, si nous traçons nos seuils d'apparition des spirales négatives en fonction des vitesses angulaires WhetWb ainsi adimensionnées (Figure 10), nous constatons que les différentes mesures se regroupent sur une seule et même courbe maîtresse. Cette propriété confirme donc que les spirales négatives sont bien le résultat d'une instabilité de cisaillement !
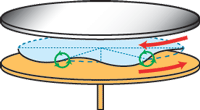
Figure 9 : Schéma de l'instabilité de cisaillement
azimutale responsable de l'apparition des spirales négatives. Dans
le référentiel lié à la rotation moyenne, l'écoulement
de base peut être vu comme une couche de cisaillement (en bleu) séparant
deux demi-espaces de rotation opposée. Cette couche se déstabilise
selon une modulation azimutale et s'enroule selon les flèches circulaires
vertes (un mode 4 est schématisé ici, c'est-à-dire
4 longueurs d'onde sont présentes sur la circonférence).
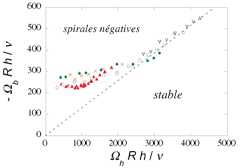
Figure 10 : Seuils d'apparition des spirales négatives
en fonction des vitesses angulaires de chacun des disques Wb
et Wh,
pour différents espaces interdisque h entre 7 et 23 mm. Le
regroupement des différentes données sur une même courbe
indique que ces structures pro-viennent d'une instabilité de cisaillement.
Notre écoulement, d'apparence si simple, présente donc maintenant deux classes d'instabilités associées à des mécanismes très différents : instabilités de couche limite (spirales positives et cercles) et instabilité de cisaillement (spirales négatives). Il est même possible, pour certaines valeurs des vitesses angulaires, d'observer simultanément ces différentes structures : ainsi, la Figure 11 montre un réseau de spirales négatives, s'étendant sur pratiquement toute la cellule, auquel se superpose un réseau de spirales positives, visible uniquement à grand rayon (cette situation correspond à la zone bleue hachurée du diagramme de la Figure 6). Du fait de leur nature différente, et donc de leur localisation différente dans l'épaisseur interdisque, ces structures se superposent sans aucune interaction apparente !

Figure 11 : Superposition d'un réseau de spirales
positives (instabilité de couche limite) et de spirales négatives
(instabilité de cisaillement).
Conclusion
La grande diversité des structures que nous venons d'observer est remarquable en regard de l'apparente simplicité de notre géométrie. Cette situation est générique des systèmes gouvernés par des équations non-linéaires, dans la classe desquels entrent les écoulements des fluides : aux solutions de bases, en général simples car possédant un grand nombre de symétries, se substituent des motifs beaucoup plus variés, pouvant parfois coexister entre eux. L'écoulement entre deux cylindres coaxiaux en rotation, d'une grande utilité pratique en rhéologie, est un autre exemple de géométrie très simple et présentant pourtant une grande variété de motifs d'instabilité.
Notre dispositif expérimental nous a permis, outre une étude détaillée des instabilités de couche limite (qui avaient déjà pu être observées expérimentalement et numériquement), de mettre en évidence un nouveau type d'instabilité, les spirales négatives, présentes uniquement en configuration contra-rotative. Motivés par ces récentes observations expérimentales, des travaux numériques sont venus récemment confirmer leur existence. Une telle étude numérique s'avère extrêmement coûteuse en temps de calcul : du fait des temps d'apparition très élevés, ces simulations doivent intégrer les équations de Navier-Stokes tridimensionnelles pendant un temps très long. C'est le travail qu'ont réalisé Olivier Daube (Université d'Evry) et Patrick Le Quéré (LIMSI, à Orsay). La Figure 12 a été obtenue dans un cylindre correspondant à une épaisseur interdisque h=20 mm, et représente les surfaces d'égale vitesse verticale. Cette quantité est sensible en particulier à l'enroulement des lignes de courant dans l'épaisseur interdisque. On y voit clairement apparaître un écoulement structuré en bras spiraux, en très bon accord avec nos observations expérimentales.
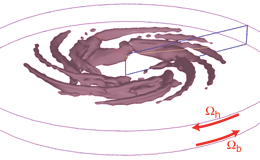
Figure 12 : Exemple de simulation numérique des
spirales négatives. Données de O. Daube et P. Le Quéré,
montrant un motif de spirales négatives à 9 bras spiraux.
Les super-ordinateurs les plus puissants sont aujourd'hui capables de calculer l'évolution temporelle de ce type d'écoulement tridimensionnel en rotation. Cette prouesse technique était encore inenvisageable il y a quelques années seulement, et ouvre la voie à des études d'intérêt pratique considérable. Parmi les applications pouvant bénéficier de ces avancées, citons les turbines des centrales hydroélectriques, ou encore les turboréacteurs utilisés en aéronautique. Cette dernière application met en jeu des vitesses de rotation considérables (plus de 10 000 tr/min), dont la simulation ne sera rendue possible qu'au prix de modélisations des phénomènes turbulents présents à de telles vitesses. De telles études nécessitent, afin d'ajuster les paramètres des modèles employés, des comparaisons avec des expériences étalons. Dans ce contexte, les récents succès des comparaisons entre simulations et expériences s'annoncent très encourageants dans la compréhension et la modélisation des écoulements en rotation.
1 On raconte qu'Einstein aurait, grâce à cette explication, contenté la curiosité de Mme Schrödinger, que son mari ne parvenait à satisfaire...
2 Cette épaisseur d est la distance sur laquelle la force centrifuge, ~ U2/r, compense la force de frottement visqueuse, ~ n U / d2 : on obtient ainsi d = (n/W)1/2.
3 Il s'agit là d'une propriété classique des phénomènes critiques au voisinage d'un point de transition.